- Connecting audio
- Audio PC
- Raspberry & Co
- All in Ones
- Bluetooth
- Chromecast
- Streaming audio player
- Music server
- USB Audio
- Real-time audio over IP
- FireWire DAC
- Multi-channel DAC
- NAS
- Remote control
- Vinyl rippers
- Acoustic materials
- Active crossover
- Active speakers
- Single driver speakers
- Invisible speakers
- Sound card
- Digital room correction
- Headphone
- Portable media players
USB cables
Cable length between full speed devices is limited to 5 meters. For a low speed device the limit is 3 meters.
As the signal degrades proportional to the length of the cable, a short cable is often recommended. Other says this put the PC to close to the USB-DAC.

A short cable
Audiophile USB cables
As file based audio is gaining momentum and many believe asynchronous USB the way to go there is a growing market for audiophile grade USB cables.
The question of course is why a cable can have any impact on sound quality.
Some say that improved jitter performance of a cable can make a difference.
Others say that the reason we use asynchronous USB is exactly to have zero input jitter at the DAC so all what is happening upstream is irrelevant cable included.[1]
Audiophile USB cables are becoming as controversial as high-end power cords.
The Limitations of digital audio processors and cables create timing
errors known as jitter, which remove portions of the audio signal and
replace them with noise and distortion. Cables tend to round off the
square waveforms of the signal, making them less clear to the processor,
thus increasing jitter. This rounding effect varies greatly among cables
and a truly superior digital audio cable can make great improvements
in sound quality.
Source: wireworldcable
Another manufacturer talking some marketing bull shit?
They do have a point.
Digital is indeed sending fully analogue electrons over a wire.
And indeed, the block pulse degrades with the length.
A good digital cable is one who minimizes this degradation.
The USB 2.0 specification lists a maximum cable length of 5 meters (~15 feet). This is marginal with the best of cables, and many "audiophile grade" cables will run into problems even with far shorter lengths. There have been many credible reports of improved sound quality with some cables, but these have almost all been in systems using Class 1 Audio, with a maximum data rate of 12 MHz. When the data rate is boosted by a factor of 40x to 480 MHz, there are very few "audiophile" cable companies that have the tools and experience to ensure good results.
Computer Audio Playback Overview - Ayre
This is an easy test.
Connect your high speed USB device, e.g. a hard disk using your audiophile
grade USB cable. If hi-speed mode (480 Mbps instead of 12 Mbps, the
old USB 1 standard) fails, it is a bad DIY digital cable not even compliant
with USB 2 standards.
 $0.78 - Monoprice USB 2.0 A Male to B Male 28/24AWG Cable - (Gold Plated) - 3ft
$0.78 - Monoprice USB 2.0 A Male to B Male 28/24AWG Cable - (Gold Plated) - 3ft
 € 11,90 LaCie 1.2 m
€ 11,90 LaCie 1.2 m
$85.00 - Wireworld Starlight 6 (1m)
Silver-clad oxygen-free copper
 $125.00 - Kimber Kable MBUSAG (1m)
$125.00 - Kimber Kable MBUSAG (1m)
Pure Silver signal conductors
(6.1%) Silver-plated copper power conductors
(6.1%) Silver-plated copper drain and shield wire
High-Density polyethylene signal conductor dielectric

$1149 - Locus Design Nucleus
1-3ft, $120 each additional foot after three
$12,000 - MasterBuilt
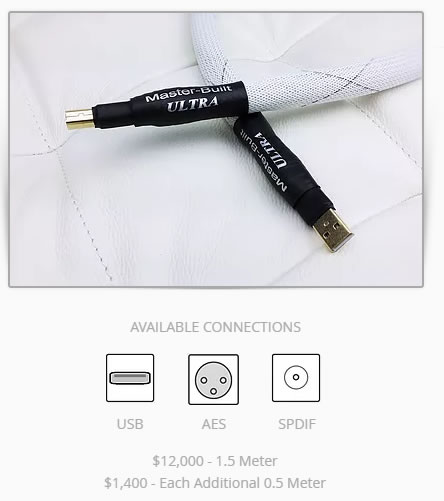

Do you smell something fishy?
Measurements
Much debate on the audio forums about USB cables, measurements are rare.
Marlene’s Musings measured USB cable. He couldn't find any measurable difference but claims to hear them in a double blind test.
Archimago couldn't measure any difference either.
AmirM did measure a small difference.
Using a J-test he measured a small difference in noise floor between a generic USB cable and a TotalDac D1 (€ 360).
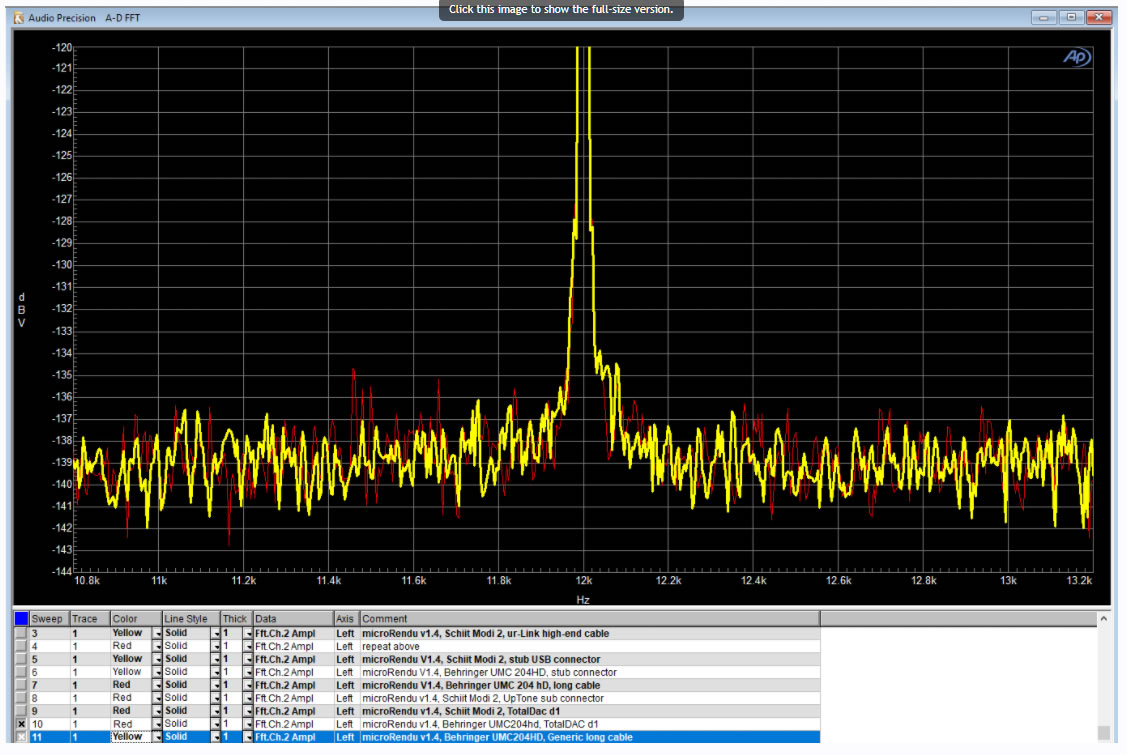
Yellow:long generic cable, red TtalDAC d1
Do observe that the scale of his screen shots is substantially magnified, showing the range -120 to -144 dBfs only. Without this, the differences are not visible.
This proofs that these differences are very small indeed and at a level probably not audible.
Anyway, his generic USB cable performed slightly better than the high-end one.
Amir again, this time a generic USB cable versus Wireworld Starlight 7 ($100)
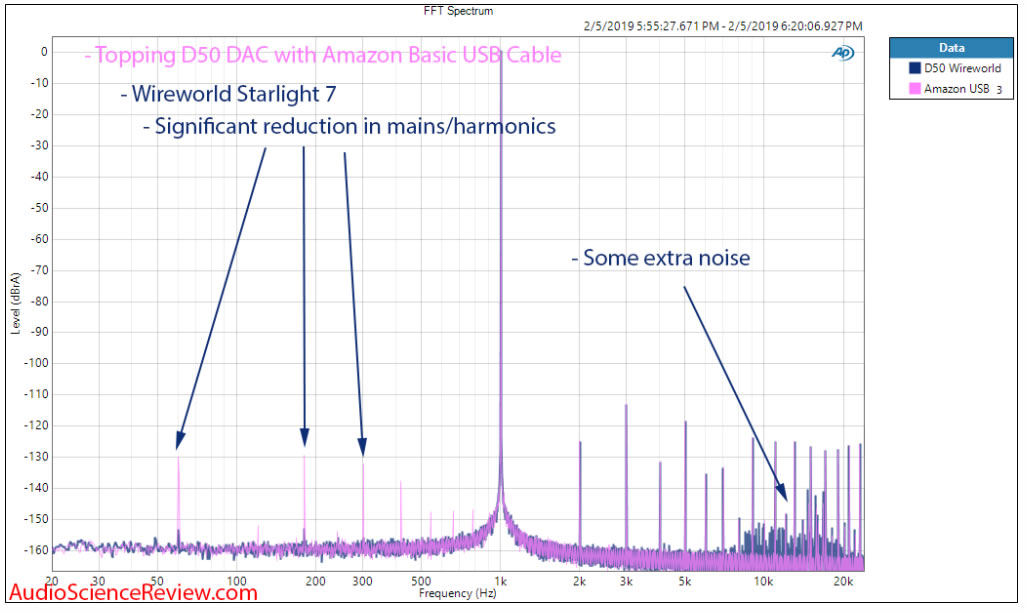
Probably not an audible difference but a measurable difference for sure.
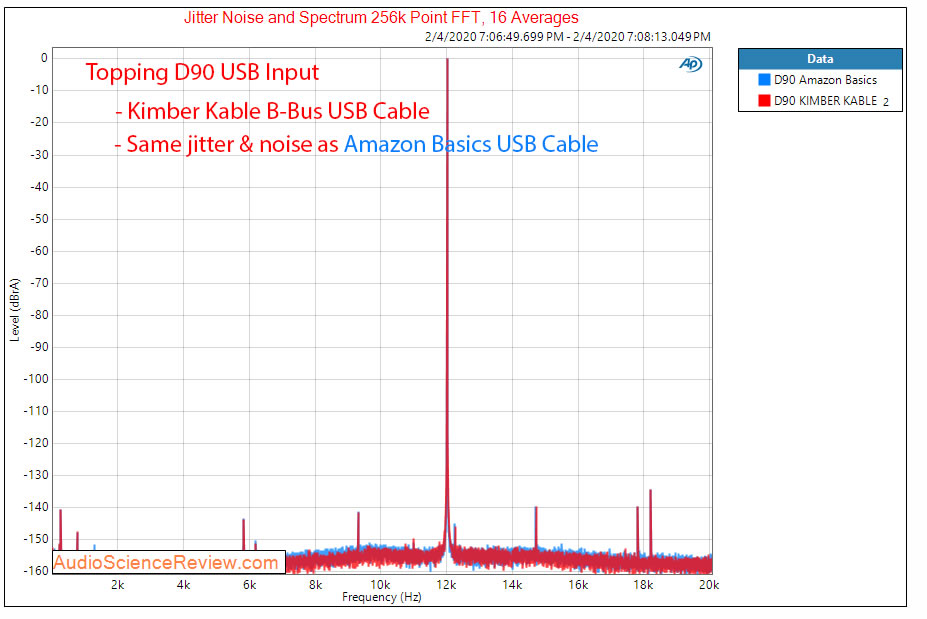
The Amazon USB cable and the $60 Kimber don't differ at all.
- Computer Audio: Is isolation as good as optimization? - What's Best Forum
- Vodoo continued: my final Statement on USB cables - Marlene's Musings
- USB Cables for Audio DAC's - Archimago's musings
- Measurement and Review of TotalDAC D1 USB Cable - AmirM
- Do USB Audio Cables Make A Difference? - AmirM
- Review and Measurements of Wireworld Starlight 7 USB Cable - AmirM
- KIMBER KABLE: Do High-end USB Cables Make A Difference? - AmirM

